What is Rotational Symmetry?
Rotational Symmetry is easiest to understand when we consider an example shape: A rectangle can be rotated about its centre by half a turn (or 180°) and the rotated shape looks exactly like the original rectangle. We therefore describe a rectangle as having rotational symmetry (of order 2, but we’ll get to that).
If you think of a child’s shape sorter toy, when the child puts in the blue circle it can go in at any angle. The green square, on the other hand, can only go in in one of four orientations.

You could lift the green square out, rotate it by 90° (a quarter turn) and drop it back in.
The red oval and the orange rectangle would also drop back in but only after a rotation of 180°.
The yellow triangle (equalateral) would drop back after 120° of rotation.
These are all said to have rotational symmetry.
But surely all shapes would fall back in after 360° of rotation?
Yes, they would; but If you need to turn the shape a full 360° before it falls back in, then it is not considered to have rotational symmetry. So this heart shape does not have rotational symmetry…

So how might this look in the GL Transfer Test?
Perhaps something like this…
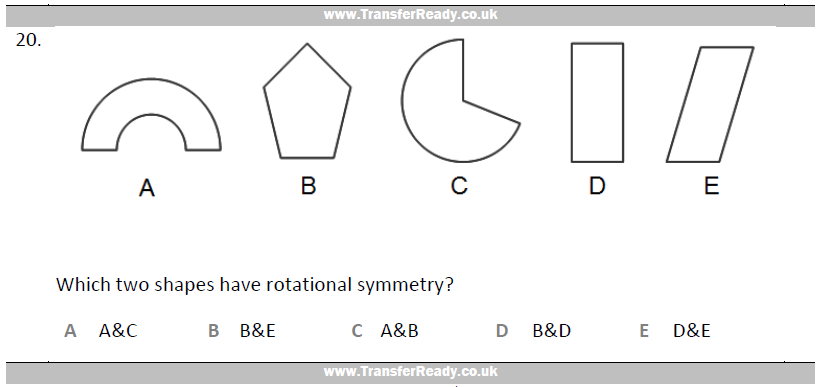
[Hint: Only shapes D and E have rotational Symmetry and both are order 2. The answer is E]
So remember, even shapes that have no rotational symmetry are order 1 – when they are rotated by a complete 360° they look the same – but these are said to have no rotational symmetry.
![]()
Now try this worksheet.
Answers:
![]()
